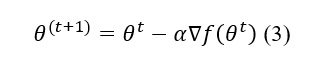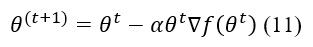Анотація. У статті розглядається вдосконалення класичної системи Ело шляхом її узагальнення та застосування методу градієнтного спуску для оптимального налаштування параметрів рейтингової моделі. Система Ело традиційно використовується для оцінювання рейтингів агентів у замкненому середовищі, однак фіксовані параметри (зокрема, коефіцієнт K) не дозволяють їй адекватно реагувати на зміну контексту або специфіку взаємодій. У статті пропонується підхід, що враховує додаткові фактори впливу на результати матчів та важливість подій, вводячи набір параметрів, які оптимізуються з використанням функції логістичних втрат як цільової функції оптимізації. Методологія передбачає поетапне оновлення параметрів згідно з модифікованим методом градієнтного спуску, що дозволяє адаптивно змінювати модель для конкретного середовища. Практична частина демонструє застосування методу на прикладі англійських футбольних турнірів з 1998 по 2024 рік, де проведено навчання та валідацію моделі на історичних даних. Такий підхід дозволяє не лише підвищити точність прогнозування, але й забезпечує більшу гнучкість системи у порівнянні з класичним підходом.
Ключові слова: система Ело, антагоністична гра, градієнтний спуск, оптимізація параметрів, машинне навчання, логістичні втрати, класифікація, параметри моделі, валідаційний датасет.
ВСТУП. Система Ело використовується для оцінювання рейтингів агентів (гравців) на основі їх взаємодії у замкненому середовищі. Вона широко використовується як рейтингова система для оцінки відносних рейтингів агентів у таких середовищах, як шахи, кіберспорт та спортивні ліги і може бути застосована до антагоністичних ігор.
Класична реалізація системи Ело[1] базується на оновленні рейтингів гравців після кожної взаємодії залежно від очікуваного та фактичного результату. Позначимо через r_ik і r_jk рейтинги агентів i та j перед k-ою взаємодією. Очікуваний результат взаємодії агента i з агентом j для агента i визначається за допомогою логістичної функції:
де Sik — фактичний результат взаємодії (наприклад, 1 при перемозі, 0 при поразці, 0.5 при нічиї), а K — коефіцієнт корекції, що визначає швидкість оновлення рейтингу. Вибір значення K є критично важливим, оскільки надто високе значення робить рейтинг нестабільним, а надто низьке — надто інерційним, не встигаючи за зміною реальних рейтингів агентів. Тому необхідно використовувати таке значення K, яке у відповідному середовищі дозволяє балансувати між стабільністю та швидкістю реакції на взаємодії.
Хваттум і Арнтцен адаптували систему Ело до футболу[2], проте в їх роботі параметри системи визначалися вручну. Аналогічний підхід використовують Ангеліні, Канділа та де Анджеліс у своїй адаптації системи[3] до тенісу. Запропонована робота має на меті узагальнити опис системи Ело та продемонструвати ефективність градієнтного спуску для налаштування рейтингових моделей у контексті прогнозування результатів.
МЕТОДОЛОГІЯ. Класичний підхід доволі простий, проте зазвичай має низку недоліків, зокрема жорстко заданий коефіцієнт K та нечутливість до особливостей ігор у різних середовищах. Зокрема, взаємодії між агентами можуть мати різну важливість, на результат взаємодії можуть впливати додаткові фактори крім рейтингу агентів. Крім того в середовищі можуть існувати окремі підсередовища, в яких агенти зазвичай взаємодіють з агентами зі свого підсередовища і лише зрідка з агентами з інших підсередовищ. З огляду на викладене, щоб зробити систему Ело оптимальною для певного середовища, виникає потреба в значно більшій кількості параметрів, і, а відтак - у налаштуванні цих параметрів шляхом пошуку оптимальних значень. Це створює підґрунтя для застосування методів оптимізації для налаштування параметрів системи, що дозволяє покращити точність прогнозів та зробити модель більш гнучкою.
Градієнтний спуск - один із найпоширеніших методів оптимізації, що використовується для мінімізації функцій втрат. Його суть полягає в тому, що ми поступово зменшуємо значення функції втрат, оновлюючи параметри в напрямку, протилежному градієнту функції втрат. У загальному вигляді[4] метод оновлює параметри згідно з рівнянням:
де α — швидкість навчання, що контролює розмір кроку оновлення, а θt – набір параметрів. Вибір значення α також є критичним: завелике значення може призвести до нестабільної збіжності, а замале — до дуже повільного навчання.
На відміну від класичного підходу, метод градієнтного спуску дозволяє адаптивно змінювати параметри в залежності від специфіки середовища. Він дозволяє побудувати модель машинного навчання, яка в процесі навчання поступово вдосконалює параметри моделі, реагуючи на похибки прогнозів і, таким чином, краще узгоджується з реальними результатами.
У контексті налаштування параметрів системи Ело ми використовуємо логістичні втрати як функцію втрат та оптимізуємо параметри системи для підвищення точності рейтингових прогнозів. Такий підхід дозволяє порівнювати передбачену ймовірність результату взаємодії з фактичним результатом, забезпечуючи врахування ступеню похибки.
Формально функція логістичних втрат визначається як:
Ця функція є стандартною для задач класифікації[5] яка застосовується у у випадку системи Ело, де необхідно моделювати ймовірність двох альтернативних результатів. Важливо, що функція логістичних втрат[6] штрафує більші помилки сильніше, коли модель надмірно впевнена у неправильному результаті. Наприклад, якщо система присвоює події з результатом y_i=1 низьку ймовірність p(y_k )≈0.1, то штраф буде значним через логарифмічну природу функції.
Завдяки своїй властивості диференційовності, ця функція зручна для застосування методів оптимізації, зокрема градієнтного спуску, що дозволяє ефективно оновлювати параметри системи Ело у напрямку зменшення помилки передбачення.
Ця функція використовувати і в якості метрики для порівняння ефективності різних варіацій системи Ело.
УЗАГАЛЬНЕНИЙ ОПИС СИСТЕМИ ЕЛО. Як зазначалося раніше, в загальному випадку на результат взаємодії агентів може впливати не лише їхні райтинги, але й певні додаткові фактори, які потрібно врахувати при розрахунку очікуваного результату взаємодії агента i з агентом j, тому це значення дорівнюватиме:
Таким чином ми бачимо, що значення функції логістичних втрат залежить від початкових рейтингів агентів, результатів взаємодій між ними, факторів впливу на ймовірність очікуваного результату взаємодії та факторів впливу на важливість події. Оскільки R1 та S є сталими, то значення функція логістичних втрат залежить від вибору параметрів g1,g2,…,gL,h1,h2,…,hL (або θ, як позначали в (3)), оптимальні значення яких потрібно підібрати для відповідного середовища.
В загальному випадку набір параметрів після кожної ітерації градієнтного спуску оновлюється (3) з однаковим коефіцієнтом. Однак для покращення збіжності параметрів з малими значеннями в даному випадку доцільніше використовувати дещо модифікований підхід:
Таким чином, параметри з великими значеннями змінюватимуться швидше і, відповідно, параметри з малими значеннями - повільніше.
Загалом, процес оптимізації параметрів моделі на основі системи Ело за допомогою градієнтного спуску включає такі кроки:
Обчислення початкових значень рейтингів: Для найдавніших доступних даних визначаються початкові рейтинги для всіх гравців або команд.
Розбиття даних: Поділ датасету на навчальну вибірку (ранні матчі) та валідаційну вибірку (останні матчі).
Обчислення градієнтів параметрів: Для кожного параметра обчислюємо градієнт
Оновлення параметрів: Нові значення параметрів обчислюються за (11).
Перевірка цільової функції на валідаційному наборі даних.
Цей підхід, на відміну від класичного методу оновлення рейтингу, дозволяє:
Динамічно адаптувати параметри під зміну рейтингів агентів.
Мінімізувати функцію втрат, що веде до кращої відповідності фактичним результатам матчів.
Зменшити вплив шуму в даних за рахунок більш згладжених оновлень параметрів.
ЗАСТОСУВАННЯ. В якості прикладу застосування розглянемо дані англійських футбольних турнірів, починаючи з сезону 1998/1999, а саме матчі Прем'єр-Ліги, Футбольної Ліги, Кубку Англії, Кубку Ліги, Суперкубку та Трофею Футбольної Ліги (матчі за участю команд поза Прем'єр-Лігою та Футбольною Лігою не розглядатимемо). Сезон 1998/1999 використовується для обрахунку початкових значень рейтингу клубів та початкового впливу фактору домашнього поля, дані з сезону 1999/2000 до сезону 2009/2010 – як навчальний датасет для обрахунку градієнтів, а дані з сезону 2010/2011 до сезону 2023/2024 – як валідаційний датасет.
Враховуючи, що кубкові турніри зазвичай мають менший престиж, ніж ліги, розглядатимемо два різні коефіцієнти корекції: один для матчів ліг (K_League), а інший – для матчів кубкових турнірів (K_Cup). Крім того, ймовірність перемоги у матчі залежить від того, на полі якої команди проходить матч (господарі мають більшу ймовірність перемоги за умови однаковості інших параметрів). Тому розглядатимемо ймовірність перемоги команди-господаря i в матчі як:
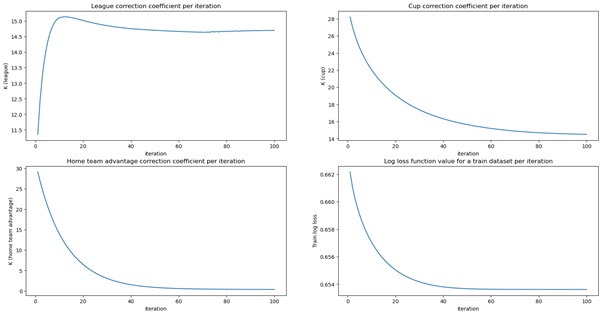
Початкові значення параметрів обираємо випадковим чином в діапазоні від 0 до 50. Значення параметрів, а також значення функції логістичних втрат для навчального датасету протягом перших 100 ітерацій наступні:
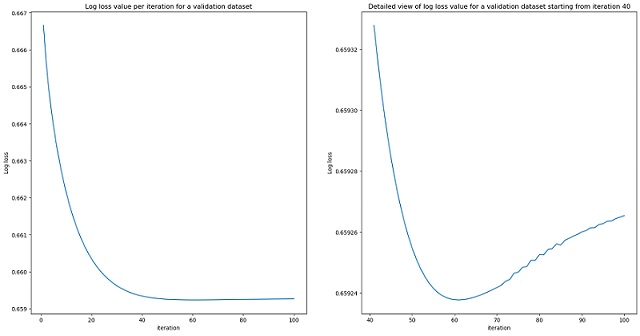
Значення функції логістичних втрат для валідаційного датасету в залежності від ітерації виглядає наступним чином (окремо розглянено деталізований графік після сорокової ітерації):
Після 61 ітерації значення функції логістичних втрат починає зростати, що означає перенавчання алгоритму, і в даному випадку має сенс застосувати ранню зупинку, щоб уникнути цього.
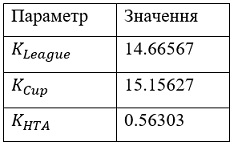
Таким чином, отримано наступні оптимальні значення параметрів:
Для цих параметрів значення цільової функції на валідаційному датасеті рівне 0.659238. В класичному підході Хваттум і Арнтцен[2] використовували значення K_League=20, не враховували матчі кубкових турнірів (KCup=0), а також використовували статичне значення HTAk=80, тобто KHTA=0. При такому підході значення функції логістичних втрат на нашому валідаційному датасеті дорівнює 0.66805. Таким чином, нам вдалося істотно покращити точність алгоритму за рахунок його розширення додатковими параметрами та використанням методу градієнтного спуску для пошуку оптимальних значень цих параметрів.
ВИСНОВКИ. Нами узагальнено систему Ело з можливістю врахування додаткових параметрів, а також адаптовано метод градієнтного спуску для пошуку оптимальних значень цих параметрів. На основі реалізації виявлено ефективність застосування методу градієнтного спуску для пошуку оптимальних значень параметрів системи Ело, що дозволяє знайти баланс між стабільністю системи та швидкістю відклику на останні взаємодії агентів. В даній статті не розглядалась детально логіка обрахунку початкових рейтингів агентів. Очевидно, цю логіку також можна параметризувати, і шукати відповідні параметри за допомогою методу градієнтного спуску. Так само, як і для логіки обрахунку рейтингу нових агентів, що зʼявляються у середовищі. Саме це буде наступною метою подальших досліджень.
Список використаних джерел:
1. A.E. Elo. (1978). The rating of chess players, past and present.
2. L. M. Hvattum, H. Arntzen. (2010). Using ELO ratings for match result prediction in association football. International Journal of Forecasting. Volume 26, Issue 3, 460-470. https://doi.org/10.1016/j.ijforecast.2009.10.002
3. G. Angelini, V. Candila, L. De Angelis. 2022. Weighted Elo rating for tennis match predictions. European Journal of Operational Research. Volume 297, Issue 1, 120-132. https://doi.org/10.1016/j.ejor.2021.04.011
4. Ruder, S. (2016). An overview of gradient descent optimization algorithms. arXiv preprint arXiv:1609.04747. https://doi.org/10.48550/arXiv.1609.04747
5. Prasetio, D. (2016, August). Predicting football match results with logistic regression. In 2016 International Conference On Advanced Informatics: Concepts, Theory And Application (ICAICTA), 1-5. IEEE. https://doi.org/10.1109/ICAICTA.2016.7803111
6. Vovk, V. (2015). The fundamental nature of the log loss function. Fields of logic and computation II: Essays dedicated To Yuri Gurevich on the Occasion of His 75th Birthday, 307-318. https://doi.org/10.48550/arXiv.1502.06254
|