|
|
|
КОМП’ЮТЕРНІ СЦЕНАРІЇ ВЗАЄМОДІЇ ЛЕГАЛЬНОЇ Й ТІНЬОВОЇ ЕКОНОМІКИ СУСПІЛЬСТВА
| |
| 17.04.2012 17:07 |
|
Автор: Коляда Юрій Васильович, к.ф.-м. наук, доцент кафедри економіко-математичного моделювання ДВНЗ «Київський національний економічний університет імені Вадима Гетьмана»; Семашко Катерина Анатоліївна, асистент, аспірант кафедри економіко-математичного моделювання ДВНЗ «Київський національний економічний університет імені Вадима Гетьмана»
|
|
[Секція 4. Економічний аналіз. Економіко-математичне моделювання;] |
У загальному випадку взаємодія легальної економіки (ЛЕ) і тіньової економіки (ТЕ) являє собою динамічний процес. Вона описується [1] системою нелінійних звичайних диференційних рівнянь
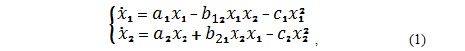
де змінні Х1=Х1(t) I X2=X2(t) відповідно описують обсяги ЛЕ і ТЕ; коефіцієнти ai(i=1,2) власні швидкості варіативності обсягів; величини bij (i;j=1,2;i≠j) стосується ступеня взаємодії двох гілок економіки; коефіцієнти сi відповідають рівням само обмеженості згадуваних обсягів. Таким чином, має місце так звана точкова математична модель (ММ) динаміки, яка отримується з використанням синергетичного способу головних пропорцій та основного принципу кінетики [1] про білінійну взаємодію складових об’єкта моделювання.
Висловлюється гіпотеза: два різновиди економіки полярні за своїм цільовим призначенням, але між ними існує певний взаємовплив (позитивний або негативний зворотний зв'язок). Зазначене описується ММ (1),
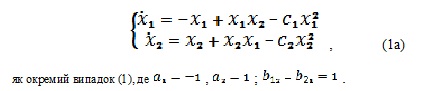
Згідно підходу наскрізного адаптивного моделювання економічної динаміки [1] спершу шукаються особливі (стаціонарні, рівноважні або критичні) точки, прирівнюючи похідні до нуля. Координати згадуваних точок є розв’язки нелінійної системи алгебраїчних рівнянь
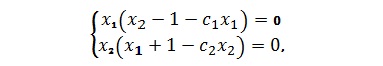
яких всього три, а саме: №1 – тривіальна (0;0); №2 – (0; 1/С2); №3 - 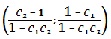 , приймаючи до уваги вимогу про додатні числові значення. Звісно, що мають виконуватися нерівності: С1< 1; С2 > 1 і С1С2<1. , приймаючи до уваги вимогу про додатні числові значення. Звісно, що мають виконуватися нерівності: С1< 1; С2 > 1 і С1С2<1.
Функціональна матриця Якобі для ММ (1а) має вигляд
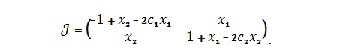
Її числові характеристики записуються: слід 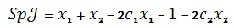 як сума елементів головної діагоналі; визначник як сума елементів головної діагоналі; визначник 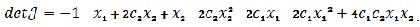 Величини Величини 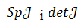 обчислюються для кожної рівноважної точки. Знаючи їх знаки, кваліфікується тип особливої точки. Наприклад, тривіальна точка є сідловка, бо обчислюються для кожної рівноважної точки. Знаючи їх знаки, кваліфікується тип особливої точки. Наприклад, тривіальна точка є сідловка, бо 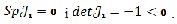
Для критичної точки №2 мають місце вирази: 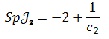 причому слід матриці додатний для С2<1/2, від’ємний для С2>1/2 і рівний нулю для причому слід матриці додатний для С2<1/2, від’ємний для С2>1/2 і рівний нулю для 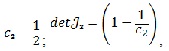 причому визначник додатній для C2>1 і тоді буде стійкий вузол (фокус); для C2<1 визначник від’ємний і буде сідловка точка (нестійка). причому визначник додатній для C2>1 і тоді буде стійкий вузол (фокус); для C2<1 визначник від’ємний і буде сідловка точка (нестійка).
Для третьої особливої точки справедливі вирази: 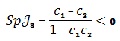 приймаючи до уваги додатність координат, тобто C2>1, C1<1 i C1C2<1, у випадку C2<1, C1>1 повинна виконуватися нерівність C1C2>1. приймаючи до уваги додатність координат, тобто C2>1, C1<1 i C1C2<1, у випадку C2<1, C1>1 повинна виконуватися нерівність C1C2>1.
Визначник матриці 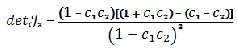 від’ємний для C2<1, C1>1 і C1C2>1, тоді буде сідловка точка; додатний для C2>1, C1<1 i C1C2<1, стійкий вузол (фокус) буде. від’ємний для C2<1, C1>1 і C1C2>1, тоді буде сідловка точка; додатний для C2>1, C1<1 i C1C2<1, стійкий вузол (фокус) буде.
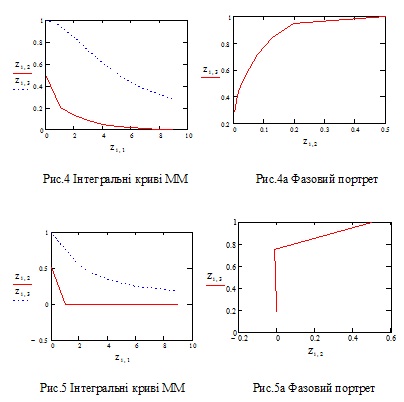
На рис. 1-5 графічно відображено результати комп’ютерного моделювання над ММ (1а) для різних числових значень коефіцієнтів C1 i C2.
C1:=0.3 C2:=1
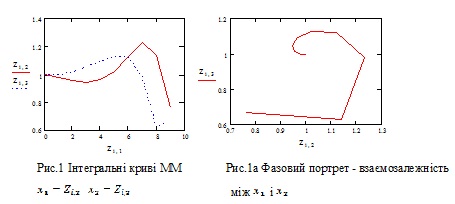
C1 :=0.5 C2 :=1.5 Має місце падіння обсягів ЛЕ і ТЕ.
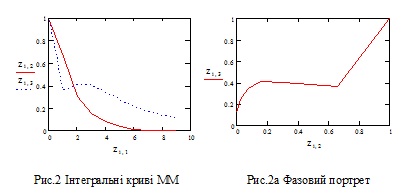
Одночасне і синхронне падіння обсягів завершується домінуванням ТЕ (Рис.3)
C1:=0.99 C2:=1
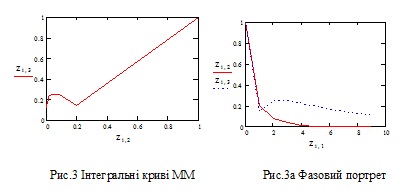
На рис. 4-5 домінує ТЕ, хоча коефіцієнти Сі мають зовсім різні числові значення, причому відношення С2/С1 падає.
Список використаної літератури:
1. Коляда Ю.В. Адаптивна парадигма моделювання економічної динаміки/ Ю.В. Коляда: монографія. - К: КНЕУ, 2011. – 297 с.
|
|
 Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License
|
|
|








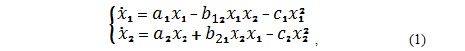
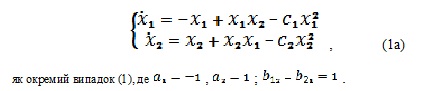
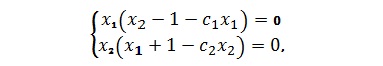
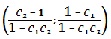 , приймаючи до уваги вимогу про додатні числові значення. Звісно, що мають виконуватися нерівності: С1< 1; С2 > 1 і С1С2<1.
, приймаючи до уваги вимогу про додатні числові значення. Звісно, що мають виконуватися нерівності: С1< 1; С2 > 1 і С1С2<1.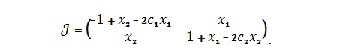
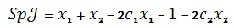 як сума елементів головної діагоналі; визначник
як сума елементів головної діагоналі; визначник 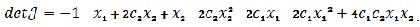 Величини
Величини 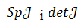 обчислюються для кожної рівноважної точки. Знаючи їх знаки, кваліфікується тип особливої точки. Наприклад, тривіальна точка є сідловка, бо
обчислюються для кожної рівноважної точки. Знаючи їх знаки, кваліфікується тип особливої точки. Наприклад, тривіальна точка є сідловка, бо 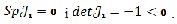
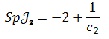 причому слід матриці додатний для С2<1/2, від’ємний для С2>1/2 і рівний нулю для
причому слід матриці додатний для С2<1/2, від’ємний для С2>1/2 і рівний нулю для 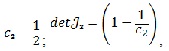 причому визначник додатній для C2>1 і тоді буде стійкий вузол (фокус); для C2<1 визначник від’ємний і буде сідловка точка (нестійка).
причому визначник додатній для C2>1 і тоді буде стійкий вузол (фокус); для C2<1 визначник від’ємний і буде сідловка точка (нестійка).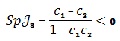 приймаючи до уваги додатність координат, тобто C2>1, C1<1 i C1C2<1, у випадку C2<1, C1>1 повинна виконуватися нерівність C1C2>1.
приймаючи до уваги додатність координат, тобто C2>1, C1<1 i C1C2<1, у випадку C2<1, C1>1 повинна виконуватися нерівність C1C2>1. 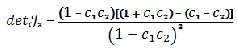 від’ємний для C2<1, C1>1 і C1C2>1, тоді буде сідловка точка; додатний для C2>1, C1<1 i C1C2<1, стійкий вузол (фокус) буде.
від’ємний для C2<1, C1>1 і C1C2>1, тоді буде сідловка точка; додатний для C2>1, C1<1 i C1C2<1, стійкий вузол (фокус) буде.


