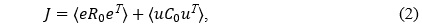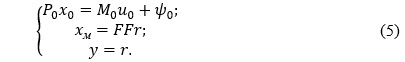Systems for simulating the natural flight of aircraft are widely used for various purposes. These include certifying aviation system sensors, configuring and testing autopilots and onboard control systems, and researching human psychophysiological characteristics, among others. The relevance of developing and creating such systems is underscored by the large number of companies engaged in developing similar systems. Virtually all design bureaus in the aerospace industry have full-scale simulation systems in their structure. Despite this, the accuracy of natural modeling of stochastic flight conditions is limited. This limitation leads to increased time, labor, and cost of developing onboard equipment. The primary reason for these limitations is the imperfection of the platform motion control system, which simulates the behavior of the simulation object.
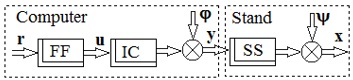
Most natural flight simulation systems for aircraft consist of a computer and a platform (test bench) for its movements. They are connected via a special interface. As shown by an analysis of literature sources [1, 2, 3], almost all of them are designed using an open-loop structure (Fig. 1).
Fig. 1. An open-loop structure
A probing signal r from a standard signal generator is fed to the input of such a system. Under the action of this signal, a vector of platform movement program signals u appears at the output of the filter block (FF). From the production of the FF block, this vector is fed to the inverse kinematics problem-solving block (IC). As a result of solving this problem, a vector of platform drive control signals y is formed at the output of the IC block. The formation of this vector is accompanied by noise (errors) when solving the inverse kinematics and interpolation problems. The vector φ represents this noise. Under the action of the components of the vector y, the platform performs movements. As a result of the movement, it occupies a position in space characterized by the vector of the platform's output coordinates, x. The movement of the platform is impeded by resistance forces, which are represented by the vector ψ. In the ideal operation of the natural flight simulation system, the vectors u and x must coincide.
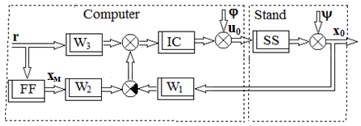
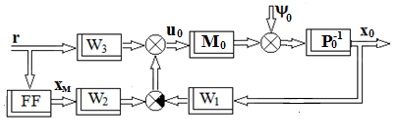
Fig. 2. A closed-loop structure
In actual system operation, vectors u and x do not coincide due to noise, interference, and the inertia of the simulator. These differences ε can be reduced in an open loop by predicting the type of vectors φ and ψ, as well as by continuously monitoring the technical characteristics of the simulator. Noise and interference vectors are usually multidimensional stochastic processes. Therefore, their prediction is difficult. Continuous monitoring of the technical condition of the simulator requires significant complication of the hardware and software parts of the simulator. Additionally, the presence of prediction and constant monitoring in an open-loop system does not guarantee complete compensation for the difference between vectors u and x. To overcome the disadvantage of the open-loop structure, a feedback control system is proposed (Fig. 2).
It is known from various literary sources, for example [4, 5], that a feedback control system with specially selected matrices W1, W2, and W3 enables the minimization of the difference between vectors u and x. Minimization occurs by compensating for noise φ and disturbances ψ, taking into account the dynamics of the stand SS and the filter FF. For such a special selection, only the appropriate synthesis method should be used. Several factors influence the choice of synthesis method. These are the nature of the change in vectors r, φ, ψ, as well as the dynamic properties of the elements of the IS, SS, FF systems (Fig. 2).
Since this article focuses on modeling stochastic aircraft motions, the synthesis method must be selected from a variety of methods for designing optimal multidimensional closed-loop control systems with random input signals. These methods can be broadly categorized into time-domain methods and frequency-domain methods.
Time domain methods for synthesizing multidimensional closed-loop optimal systems [5–7] are used when the following conditions are met:
- the stand model is presented in the state space;
- the stand is a fully controlled and observable control object;
- the vectors r, φ, ψ are stationary centered random processes of the white noise type;
- the transfer functions matrix W3 is equal to the zero matrix;
- the quality functional is equal to the vectors ε and y components' variances weighted sum.
Frequency domain methods for synthesizing multidimensional closed-loop optimal systems [8, 9] are used when the following conditions are met:
- the stand model can be presented both in the state space or systems of ordinary equations with zero initial states;
- the stand is a fully controlled and observable control object;
- the vectors r, φ, ψ are stationary centered color noise type random processes;
- the transfer functions matrix W3 is equal to the zero matrix;
- the quality functional is equal to the vectors ε and y components' variances weighted sum.
As is known from various sources, for example [10-13], at each stage of flight, the aircraft oscillates around a given trajectory. These oscillations usually belong to a set of multidimensional stationary random processes. The dynamics of these processes differ significantly from white noise. In addition, the identification of the dynamics of perturbations (ψ) and noise (φ) showed [10] that they also belong to a similar set of random processes.
In this regard, the use of time methods requires an increase in the number of state variables while keeping the size of the control signal vector unchanged. As a result, the effect of loss of observability and controllability of the installation may occur. The use of existing frequency methods, in turn, is limited to control systems that do not have a transfer function matrix W3 (Fig. 2). Consequently, a new task arises: the synthesis of an optimal multidimensional control system.
Let the dynamics of the platform be described by a system of ordinary differential equations with constant coefficients of the form
where P0 is a polynomial matrix of dimension n0×n0 from the differentiation operator p;
x0 is the vector of coordinates defining the stand platform position, which has dimension n0;
M0 is a polynomial matrix of dimension n0×m0 from the differentiation operator p;
u0 is the stand drives control signals vector, which has dimension m0;
ψ0 is the disturbance vector.
Let us also assume that the inverse kinematics problem is solved in the system with sufficient accuracy; therefore, the matrix of transfer functions IC is equal to unity, and the interpolation noise φ is sufficiently small. In this case, the structural diagram of the system (Fig. 2) is simplified to the form of Fig. 3.
Fig. 3. Asymplified closed loop structure
The probing signals vector r is a vector of uncorrelated unit-intensity white noises. The disturbance vector ψ0 is a centered stationary random process with a known transposed matrix of spectral densities SψψТ. In this case, the synthesis problem is to find, for given matrices FF, M0, P0 and SψψТ, such controller transfer function matrices W1, W2, W3, which ensure the following two conditions:
- the closed-loop system (Fig. 3) is stable;
- the following quality criterion reaches a minimum
where e – a modeling errors vector
R0 – a positively defined weight matrix;
u – a control signal vector
С0 – a non-negatively defined weight matrix;
Т - a transposition sign.
To solve the problem, the structural diagram in Fig. 3 was considered, and a system of equations was compiled. It connects the Fourier images of the signal vectors at the input and output of the system under zero initial conditions and has the form
Representation of the transfer function matrix FF as a product of two polynomial matrices
using left-side pole removal [8] or MFD decomposition [14], allowed one to rewrite the equations system (4) as follows
The presented material demonstrates the potential for significantly enhancing the accuracy of aircraft flight dynamics modeling using a simulation platform in laboratory conditions. To achieve this goal, it is proposed to use a feedback control system, the regulator of which should consist of three parts. The search for such controller transfer functions that ensure stability and high-quality simulation can be carried out using methods for synthesizing optimal multidimensional systems for stabilizing the motion of a rigid body. To ensure this possibility, an original method of structural transformations has been developed and presented. It allows the development of a platform control system that simulates the spatial movements of an aircraft in laboratory conditions.
REFERENCES
1. Науменко К.И. Наблюдение и управление движением динамических систем. - Киев: Наукова думка, 1984. – 208с.
2. Computational Modelling and Simulation of Aircraft and the Environment Vol . 1: Platform Kinematics and Synthetic Environment D. J. Diston John Wiley and Sons, The Atrium, Southern Gate, Chichester, West Sussex, PO19 8SQ, UK. 2009. 356pp.
3. El-Sheimy, N., Hou, H., and Niu, X. Analysis and modeling of inertial sensors using Allan variance. IEEE Transactions on Instrumentation and Measurement. 2008. vol. 57. no. 1. P. 140–149.
4. Richard C. Dorf, Robert H. Bishop, Modern Control Systems. Addison-Wesley, 1998. 800 p.
5. Charles L. Phillips, Royes D. Harbor, Feedback Control Systems. Prentice Hall Upper Saddle River, New Jersey, 2000. 616 p.
6. Okko H. Bosgra, Huibert Kwakernaak, Gjerrit Meinsma “Design Methods for Control Systems”. Notes for a course of the Dutch Institute of Systems and Control, Winter term 2005–2006.
7. Chi-Tsong Chen, “Linear Systems Theory,” Third Edition, New York: Oxford University Press, 1999. 331 p.
8. F.A. Aliev, V.B. Larin “Optimization of Linear Control Systems. Analytical Methods and Computational Algorithms.” OPA (Overseas Publishers Association) N.V., 1998.
9. Блохин Л.М., Осадчй С.І., Дідик О.К., Віхрова Л.Г., Каліч В.М. Технології конструювання конкурентоспроможних комплексів керування стохастичним рухом обєктів: монографія під ред. С.І. Осадчого. – Кропивницький: Видавець Лисенко В.Ф. 2023. 292 с.
10. Thomas R. Yechout, Introduction to Aircraft Flight Mechanics: Performance, Static Stability, Dynamic Stability, and Classical Feedback Control. AIAA Education Series. Editor-in-Chief Joseph A. Schetz. American Institute of Aeronautics and Astronautics, Inc.1801 Alexander Bell Drive, Reston, VA 20191-4344 – 631 p.
11. Flying Qualities of Piloted Aircraft. Department of Defense Handbook. MIL-HDBK-1797B. Washington, DC: U.S. Department of Defense, 2012.
12. Hoblit, Frederic M., Gust Loads on Aircraft: Concepts and Applications. Reston, VA: AIAA Education Series, 1988.
13. Osadchiy S.I. Combined method for the synthesis of optimal stabilization systems of multidimensional moving objects under stationary random impacts / S.I. Osadchiy, V.A. Zozulya // Journal of Automation and Information Sciences. Vol. 45, 2013, Issue 6. pp. 25-35.
14. Kucera V. Discrete line control: the polynomial equation approach. – Praha: Akademia, 1979. – 206 p.
|