Introduction. When solving the problems of technical diagnostics of pipeline systems, researchers usually deal with small perturbations of impacts on these systems, which allows them to continue operating facilities without disrupting technological modes. The parameters that change little but still affect the efficiency of oil and gas transportation pipelines include small hydrocarbon leaks, changes in the characteristics of transported products, such as their dynamic viscosity, and changes in the geometry of the cross-section, such as its ovalization or reduction of the internal radius due to the deposition of accompanying products. In this case, the loss of the transportation product is relatively small – up to 0.5%.
Problem statement. Studying the technical condition of complex pipelines systems that have been in operation for a long time, in particular in the tasks of their technical diagnostics, there are often cases when the occurrence of emergency situations is due to the presence of small disturbances acting on the system. In mathematical modeling of such phenomena, as a rule, there are problems in which either systems of equations or boundary and initial conditions are subjected to certain perturbations, the characteristics of which are small compared to the characteristic values of the quantities under study, since large perturbations of the initial conditions usually necessitate the choice of other models to describe the phenomena - a commentary on this can be made by models for estimating flow parameters with small leaks [1] and models of flow at pipeline rupture [2]. Therefore, technical diagnostics tasks and their corresponding mathematical models are closely related to the stability of the corresponding physical processes [3].
It should be noted that the study of hydrodynamic stability in the zone of small leaks is important from two aspects affecting energy efficiency: firstly, the amount of transported hydrocarbon loss is estimated, and secondly, the flow structure in the presence of small leaks of varying intensity is studied in terms of the emergence of turbulent flow zones, which can actually reduce the useful diameter of the pipeline.
Thus, the aim of the study is a mathematical modeling of process fluid flow in a pipeline in the presence of leaks through the surface at different configurations, for which the system of Navier-Stokes equations is numerically integrated, the stability parameters of numerical schemes are investigated, informative parameters are selected to determine the leakage zones of influence, and the limits of the model's use are set before the flow transitions to the turbulent regime.
Results. The flow of products in pipelines can be described using the Navier-Stokes system of equations written in a cylindrical coordinate system [4]. However, the peculiarities of pipeline systems in terms of their geometry, as well as the symmetry of the flow, the local nature of the zone of small leaks, allow us to reduce the dimensionality of the problem. Thus, it can be assumed that we are considering a two-dimensional flow of a viscous fluid in a channel with a wall in which there is a leakage of fluid through the surface, assuming that the flow is considered stationary. This is true, in particular, for quasi-stationary processes, when it is assumed that the characteristics of the modeled flow change little with time.
Analyzing the behavior of the longitudinal velocity component in the near-wall zone, we can note a pattern that depends on the leakage rate: the higher the leakage rate, the faster the monotonicity of the velocity field on the leakage side is broken.
The greater the leakage rate, the faster the flow reacts to it by changing the monotonicity of the velocity in the near-wall zone. At certain leakage rates (V<0.5), there is no loss of flow stability at all, which is a negative point, since it actually means that there is no reaction from the system under study to the presence of small leaks; at velocities greater than these, the coordinate of flow stability loss approaches the location of the defect faster, the greater the fluid leakage rate. As the leakage rate increases, the distribution pattern of the longitudinal velocity component gradient in the near-wall zone at different leakage rates becomes different - the flow stability is lost, which can be explained by the loss of flow stability due to the occurrence of turbulent flow effects and the possible loss of stability of the difference method.
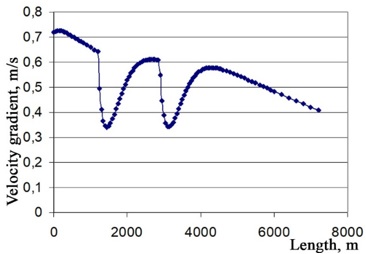
Figs. 1 show that the developed model and the numerical scheme for its implementation can be used to diagnose small leaks located at a certain distance from each other.
Fig.1 Dependence between the size of the small disturbance impact zone in the presence of several leaks of different intensity - coordinates of leaks x=1.2 km and x=2.88 km at a speed of 0.2 m/s
The stability of the scheme is not affected, although the issue of detecting multiple leaks requires more detailed study.
To improve the efficiency of the gas transportation system, it is necessary to take measures to reduce the resistance of the pipe walls, which would reduce the cost of maintaining a pressure level that would guarantee the required throughput of the system.
Conclusions. When implementing the developed model, the following typical questions arise: is it possible to identify the critical parameters at which the physical process under study loses stability, provided that the characteristics of this process are unknown and are determined by solving a certain boundary value problem. It is also necessary to determine whether the loss of stability in numerical modeling means an incorrectness of the discretized problem or a certain process occurring in the physical body under study (boundary layer separation, water hammer, turbulent effects).
Based on the results of numerical modeling of fluid flow through a channel with leakage through the surface, a method for estimating the coordinate of the leakage point and its dependence on the leakage rate is established. It has been confirmed that the problems of technical diagnostics of systems for various purposes are, from a mathematical point of view, problems of studying the stability of the corresponding processes and numerical schemes for implementing models of such processes.
References
1. Volovetskyi V.B., Doroshenko Y.V., Kogut G.M., Dzhus A.P., Rybitskyi I.V., Doroshenko J.I., Shchyrba O.M. Investigation of gas gathering pipelines operation efficiency and selection of improvement methods. Journal of Achievements in Materials and Manufacturing Engineering. Volume 107, Issue 2, Pages 59–74. 2021.
2. Doroshenko, Y., Rybitskyi, I. Investigation of the influence of the gas pipeline tee geometry on hydraulic energy loss of gas pipeline systems. Eastern-European Journal of Enterprise Technologies. Volume 1, Issue 8-103, 2020, Pages 28-34.
3. Larson R.G. Instabilities in viscoelastic flows. Rheol. Acta, 1992. V. 31. No 3. P. 213-263.
4. Mathematical modelling of the process of pipeline deformation through which gas-liquid mixtures with aggressive components are transported. Oliynyk, A.P. Feshanych, L.I. Grygorchuk, G.V. Journal of Achievements in Materials and Manufacturing Engineering, 2022, 111(2), pp. 57–63.
|
Голосування 
Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License
Знайшли помилку? Виділіть помилковий текст мишкою і натисніть Ctrl + Enter