Marketing capital allocation often relies on observational correlations that cannot support investment decisions under uncertainty. Platforms optimize for their own objectives, and naive before–after or matched comparisons confound selection and seasonality. Large-scale field experiments show that observational models frequently disagree with randomized benchmarks by material margins, which makes lift claims fragile and capital allocation noisy [2].
This abstract proposes a Ground Truth Protocol that turns causal lift into an investment-grade metric. Let the business outcome be Y per unit of analysis, and let the ad spend be S. Treatment assignment is T∈0,1. Causal lift is defined as the average treatment effect τ=E[Y(1)-Y(0)], where Y(1) and Y(0) are potential outcomes and E[⋅] denotes expectation. For capital allocation, report incremental return on ad spend as 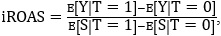 where the denominator is the incremental spend. Symbols Y, S, and T are as defined above. where the denominator is the incremental spend. Symbols Y, S, and T are as defined above.
Design primitives. Protocol execution starts with units, interference, power, and priors. Choose units that minimize spillovers across cells; geographic clusters are practical and privacy-safe. When people move between regions, geographic clustering algorithms and robust paired designs reduce contamination and heterogeneity, improving statistical efficiency in geo experiments [1], [4].
Identification toolkit. Where full randomization is feasible, run randomized geo or cluster trials and estimate τ directly with difference-in-means. With small numbers of heterogeneous regions or imperfect balance, use augmented synthetic control to de-bias the counterfactual trajectory. In this approach, a synthetic control is first fit to pre-treatment outcomes, then corrected with an outcome model to reduce bias from inexact pre-period fit. Empirically and theoretically, this improves estimation error bounds relative to vanilla synthetic control [1].
When programs scale in waves across markets, apply synthetic controls with staggered adoption and partially pooled weights to control both per-unit imbalance and average imbalance. This generalization provides finite-sample error bounds that standard two-way fixed effects regressions can violate under treatment heterogeneity [5].
Estimation details. For a two-arm geo trial with paired regions i=1,…,n, define indicators 1{T_i=1} for treatment. A variance-robust paired estimator trims poorly matched pairs to stabilize heavy-tailed outcomes and yields interpretable confidence intervals for iROAS in small-n settings [4].
In the fraction above, 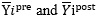 are pre and post means for outcome Y in region 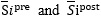 are the corresponding means for spend S, and w i are nonnegative weights that implement trimming or augmented adjustments.
Decision rules for capital allocation. Convert 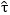 into iROAS and report its two-sided confidence interval. Approve incremental budget only if the lower bound of "iROAS" exceeds the weighted average cost of capital adjusted for working-capital frictions. Maintain a pre-registered decision policy to prevent ex post re-interpretation.
Governance and reproducibility. Maintain immutable artifacts: design doc, randomization seed, code, analysis plan, and a single source of truth dataset. When repeated tests are required, use staggered adoption or rolling geo designs and pool results with meta-analytic weighting to reduce variance while controlling for temporal drift [5].
Operational note. During experiment windows, platform-level controls can be used as instrumentation to stabilize spend exposure without contaminating identification. For example, portfolio bid strategies can cap extreme CPCs across matched campaigns, mitigating outlier auctions while preserving randomization integrity. In practice, portfolio strategies allow maximum CPC limits under Target CPA or Target ROAS and consolidate sparse signals, which reduces variance in experimental exposure [3].
Why not rely on sophisticated observational models. Evidence from fifteen at-scale experiments shows that even advanced observational estimators can diverge from randomized ground truth by factors large enough to reverse investment decisions. This gap persists despite rich covariates, which implies that identification rather than prediction governs credibility [2].
Limits. When interference is pervasive or macro shocks dominate, experiments may be underpowered. In those cases, augmented synthetic controls with careful placebo checks and sensitivity bands are second-best, provided pre-period fit and model diagnostics meet pre-specified thresholds [1].
References
1. Ben-Michael E., Feller A., Rothstein J. The Augmented Synthetic Control Method. Journal of the American Statistical Association. 2021. Vol. 116, no. 536, pp. 1789-1803. DOI: 10.1080/01621459.2021.1929245.
2. Gordon B., Zettelmeyer F., Bhargava N., Chapsky D. A Comparison of Approaches to Advertising Measurement: Evidence from Big Field Experiments at Facebook. Marketing Science. 2019. Vol. 38, no. 2, pp. 193-225. DOI: 10.1287/mksc.2018.1135.
3. Ivitskiy I. Mastering Google Ads Portfolio Bid Strategies: A Definitive Guide. Doctor Ads Blog. 28 June 2025. Available at: https://blog.thedoctorads.com/mastering-google-ads-portfolio-bid-strategies/ (Accessed: 16 September 2025).
4. Chen A., Longfils M., Remy N. Trimmed Match Design for Randomized Paired Geo Experiments. arXiv preprint. 2021. arXiv:2105.07060. Available at: https://arxiv.org/abs/2105.07060 (Accessed: 16 September 2025).
5. Ben-Michael E., Feller A., Rothstein J. Synthetic Controls with Staggered Adoption. Journal of the Royal Statistical Society: Series B. 2022. Vol. 84, no. 2, pp. 351-381. DOI: 10.1111/rssb.12448.
|








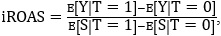
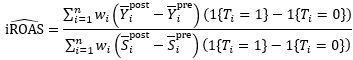
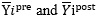 are pre and post means for outcome Y in region
are pre and post means for outcome Y in region 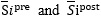 are the corresponding means for spend S, and wi are nonnegative weights that implement trimming or augmented adjustments.
are the corresponding means for spend S, and wi are nonnegative weights that implement trimming or augmented adjustments.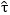 into iROAS and report its two-sided confidence interval. Approve incremental budget only if the lower bound of "iROAS" exceeds the weighted average cost of capital adjusted for working-capital frictions. Maintain a pre-registered decision policy to prevent ex post re-interpretation.
into iROAS and report its two-sided confidence interval. Approve incremental budget only if the lower bound of "iROAS" exceeds the weighted average cost of capital adjusted for working-capital frictions. Maintain a pre-registered decision policy to prevent ex post re-interpretation.