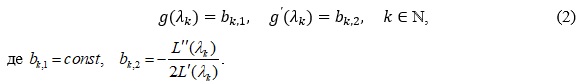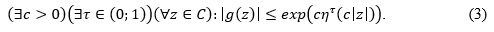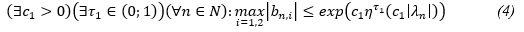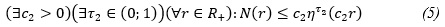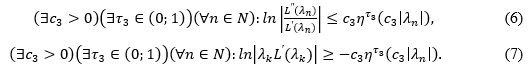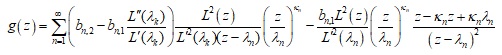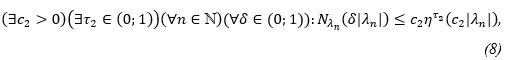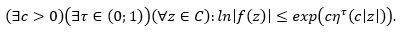|
|
|
ПРО КРАТНУ ІНТЕРПОЛЯЦІЙНУ ЗАДАЧУ ТА РОЗВ’ЯЗОК ЛІНІЙНОГО ОДНОРІДНОГО ДИФЕРЕНЦІАЛЬНОГО РІВНЯННЯ ДРУГОГО ПОРЯДКУ З ЦІЛИМИ КОЕФІЦІЄНТАМИ
| |
| 30.11.2023 17:35 |
|
Автор: Шепарович Ірина Богданівна, кандидат фізико-математичних наук, Дрогобицький державний педагогічний університет імені Івана Франка;
Карпин Захар Васильович, магістр, Дрогобицький державний педагогічний університет імені Івана Франка
|
|
[25. Фізико-математичні науки;] |
Розглянемо диференційне рівняння (ЛОДР)
Сформулюємо задачу: «Чи існує ціла трансцендентна функція a0 (z), така що (λk) є послідовністю нулів розв’язку рівняння (1)?».
Одним з перших на це запитання дав ствердну відповідь В. Седа [1]. Результати В. Седи розвинені в багатьох роботах. Так, С. Банк [2] отримав необхідні та достатні умови на послідовність (λk), за яких існує ціла трансцендентна функція a 0 (z) порядку 0 така, що рівняння (1) має розв’язок f, для якого (λk) є послідовністю нулів. У 2019 році в статті [3] отримано точніші результати у випадку, коли коефіцієнт a 0 (z) є цілою функцією нульового порядку, а послідовність (λ k ) нулів розв’язку рівняння (1) задовольняє умову 
Розв’язок (1) будується, у вигляді f=Leg, де L - ціла функція, для якої (λk) - послідовність простих нулів, g - деяка ціла функція. Тому дана задача зводиться до знаходження умов існування розв’язку інтерполяційної задачі.
Нехай η:[0;+∞)→(0;+∞) зростаюча додатна функція, для якої функція lnη (r) є опуклою відносно на проміжку [1;+∞); (λ n ) – послідовність різних комплексних чисел таких, що  і  - лічильні функції нулів в околі 0 і в околі точки z, відповідно 
Знайдемо умови на послідовність (λk), за яких інтерполяційна задача (2) має розв’язок в класі цілих функцій скінченного η-порядку, тобто таких, що задовольняють умову
Справедливими є твердження.
Теорема 1. Для того, щоб для кожної послідовності комплексних чисел, що задовольняють умову
існувала ціла функція g з класу (3), що задовольняє (2),
необхідно і досить, щоб
і для деякої цілої функції L з класу (3), яка має в точках прості нулі, виконувалися умови
Зазначимо, що існування такої функції L з класу (3) з нулями в точках λ доведено в [4]. Інтерполюючу функцію g(z) будуємо у вигляді ряду
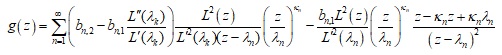
(Тут – деяка послідовність натуральних чисел, вибрана так, щоб цей ряд був збіжним).
Лема 2. Якщо для послідовності нулів (λn) деякої цілої функції L з класу (3) виконуються умови (5) і
то виконуються умови (6) і (7).
Теорема 3. Якщо послідовність (λk ) задовольняє (5) і (8), то існує така ціла функція a0 (z) з класу (3), що диференціальне рівняння (1) має цілий розв’язок f(z), для якого (λk) є послідовністю нулів і
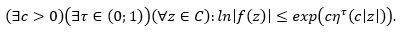
Наведемо приклад послідовності (λn), що задовольняє умови (5), (6), (7) а, отже, і (8), і є послідовністю нулів розв’язку ЛОДР другого порядку, коефіцієнти якиго є цілими і належать до класу (3).
Теорема 4. Кожна послідовність (λ n) така, що  задовольняє умови (5) і (8), яка б не була функція η така, що lnη (r) є опуклою відносно ln r на проміжку [1;+∞) 
Список літератури
1.Šeda V. O niektorých vlastnostiach rišeni diferenciálnej rovnice y″=Q(z)y, , Q(z)≡ ̸0 je celá funkcia, Acta F.R.N. Univ. Comen. Mathem, 4 (1959), 223–253.
2.Bank S. A note on the zero–sequences of solutions of linear differential equations, Results in Mathematics, 13 (1988), 1–10.
3.B. Vynnyts'kyi, I. Sheparovych, On interpolation problem with derivative in the space of entire functions with fast-growing interpolation knots, Mat. Stud., 51 (2019), №1, 51 – 58.
4.Винницький Б.В., Шепарович І.Б. Про інтерполяційні послідовності деяких класів цілих функцій, Мат. студ. 12 (1999), №1, 76 – 84.
|
|
 Ця робота ліцензується відповідно до Creative Commons Attribution 4.0 International License
|
|
|
Голосування 
Знайшли помилку? Виділіть помилковий текст мишкою і натисніть Ctrl + Enter